|
Grécia:
A Escola Pitagórica
Fundado pela lendária figura de Pitágoras,
não sabemos bem desde quando ou até quando o pitagorismo foi uma escola para
iniciados ou para uma elite esotérica reduzida. Este aspecto do pitagorismo se
deve à sua ligação com o orfismo (de Orfeu ), que tinha essas características.
A verdade é que, desde cedo, os pitagóricos
se voltaram para o número natural. Analisaram-no sob todas as formas. A
importância que atribuíram aos números, associada ao caráter místico da Escola,
conduziu os pitagóricos a verem nos números mais do que uma criação da mente
humana ou um ludismo inteligente.
Eles descobriram forças nos números,
propriedades eficientes, ações sobre a vida, poderes proféticos. E chegaram a
considerar que as coisas eram feitas de números, que os números eram a sua
FÍSIS. Eles são os primeiros que, com suficiente clareza, colocam a importância
do número:
Todas as coisas têm um número e nada se
pode compreender sem ele, diz Filolau.
A História tem de reconhecer nos
pitagóricos os primeiros a vislumbrar a importância do quantitativo(futuro da
ciência) e o fato de que o conhecimento quantitativo é mais completo e engloba
o qualitativo. Assim, pois, Pitágoras e Heráclito são precursores da Dialética
moderna.
Para relacionar um número a cada coisa, os
pitagóricos acreditaram na existência de mônadas, unidades mínimas, de forma
que cada coisa seria formada por um número inteiro de mônadas. A Escola
apresentou mais de uma demonstração do chamado Teorema de Pitágoras, que será
dispensada aqui, por ser bastante conhecida. Parece, entretanto, que este
teorema já era conhecido de egípcios e babilônicos.
Os pitagóricos relacionavam números com
fatos e entidades. Por exemplo, 3 era o número da Justiça e 4 o do casamento;
1(um) é a união, a coincidência entre o finito e o infinito (?).
Criaram, também, os conceitos de números
abundantes, deficientes e perfeitos:
a) Abundantes: são aqueles cuja soma dos
seus divisores é maior do que ele. Por exemplo, 12 admite os divisores 1, 2, 3,
4, 6, que somam 16.
b) Deficientes, cujos divisores apresentam
soma menor que o número. Por exemplo, 8 admite os divisores 1, 2, 4, que somam
7.
c) Perfeitos, cujos divisores têm soma
igual ao número dado: 496 é divisível por 1, 2, 4, 8, 16, 31, 62, 124, 248, que
somam 496!!
É claro que estes números sempre se
relacionavam com influências mágicas. Modelarmente perfeito e, por isso, pleno
de magia era o número 6, cuja soma (1+2+3) e cuja multiplicação (1.2.3) dos
divisores produzem ambas o número 6.
Também é mágico o número dez (tetrarkys):
1+2+3+4.
A orientação dos números em formas
determinadas é o que foi chamado de séries gnômicas.
A distribuição dos números ímpares 1+3+5+7+... conduz a figuras
quadradas e a somas que são segundas potências de números.
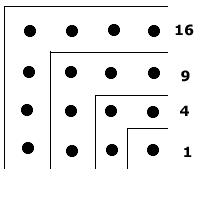
Daí por que estas segundas potências são
chamadas quadrados dos números:
|
Notemos que as somas 1, 4, 9, 16 são
quadrados, porque resultam de figuras com a forma de quadrado.
1 = 12
1 + 3 = 22
1 + 3 + 5 = 32
1 + 3 + 5 + 7= 42
1 + 3 + 5 + 7 + 9= 52
Hoje, escreveríamos: S = n2
|
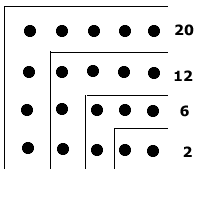
A distribuiçao dos números pares, por
sua vez, forma um retângulo (números retangulares):
|
Notando que:
2 = 1+ 12
6 = 2+ 22
12 = 3+ 32
...
Nossa expressão geral seria:
N = n+ n2
Os números 2, 6, 12, 20....são chamados
números retangulares.
|
Finalmente, a distribuição dos números
naturais forma um triângulo e, por isso, eram chamados, pelos pitagóricos, de
números triangulares.
o
1
o
o 3
o o
o 6
o o o
o 10
o o o
o o 15
Notando que:
1 = 1x2/2
3 = 2x3/2
6 = 3x4/2
10 = 4x5/2
...
a nossa expressão geral para
números como 1, 3, 6, 10, 15.....seria:
n = n (n+1)/2
As Médias Aritmética, Geométrica e
Harmônica (ou Subcontrária)
Os pitagóricos apresentaram essas três
conhecidas médias de forma bastante curiosa. Nas expressões seguintes,
considere que a média é sempre representada pela letra b:
Média Aritmética
(a-b)/(b-c) = a/a
Esta curiosa forma de escrever é
equivalente a que h oje
fazemos:
b= (a+c)/2
Média Geométrica
(a-b)/(b-c) = a/b
Note o leitor que dessa sentença resulta
que b 2 = ac.
Hoje, fazemos: b = (ac)1/2
Média Harmônica
(a-b)/(b-c) = a/c donde resulta: b=
2ac/(a+c)
que é o mesmo que obtemos hoje, ao
definir a média harmônica entre a e c pela fórmula:
b = 2 / (1/a + 1/c)
Nicômaco de Gerasa (séc. I DC) escreve:
A proporção harmônica se exprime, de
ordinário, por frações, quando relacionada com a música que, segundo a lenda,
deu ensejo à sua descoberta.
Exemplo: 6, 8, 12 ou 1, 4/3, 2
O nome subcontrária provém do fato de que,
se b é média harmônica entre a e c, então 1/b é média aritmética entre 1/a e
1/c.
Exemplo: 6, 8, 12 e 1/6, 1/8 e 1/12
Note-se a relação entre esta média
harmônica e o cubo, figura perfeita. A grande glória para os pitagóricos foi
verificar que os números 6 e 12 e as suas médias correspondiam aos comprimentos
das cordas dos instrumentos musicais: a lira tetracórdio dos gregos tinha
cordas na proporção: 6 : 8 : 9 : 12 ou 1 : 4/3 : 3/2 : 2
Quando tangidas estas cordas (mantidas
constantes a constituição e o diâmetro), fornecem,respectivamente, as notas do,
fá, sol e do(de 8.ª ), resultando, entre duas notas consecutivas, um intervalo
musical de Quarta; entre duas alternadas, um intervalo de Quinta; e entre os
dois extremos, um intervalo de Oitava:
DÓ FÁ
SOL DÓ
6
8
9
12
!<--quarta--->!
|
!<----------quinta---->
| |
<--------------------oitava----------------->|
É provável que o som de percussão (a música primitiva) tenha sido superado
inicialmente pela lira monocórdio (com o instrumentista fazendo os intervalos
com os dedos), vindo, depois, a lira tetracórdio, a lira heptacórdio, a
decacórdio e a dodecacórdio.
O Número Irracional
Não se sabe se foram os pitagóricos ou os
seus críticos de Eléia que vislumbraram por vez primeira o número irracional.
Para visualizar isso, considere um
triângulo retângulo de dois catetos iguais:
Vamos partir do conhecido Teorema de
Pitágoras, que dá o valor da hipotenusa em função dos catetos, através da
fórmula:
a2 = b2 + c2
Sendo b= c, temos:
a2
= b2 + b2
a2 = 2b2
Vamos supor que a hipotenusa a e o cateto b sejam
comensuráveis, isto é, que exista o racional m/n irredutível, tal que:
a = (m/n) b
Seja, por exemplo, m par. Então, n terá que
ser ímpar, pois trata-se de uma fração irredutível.
Por Pitágoras, sabemos que:
a2 = 2b2
elevando ao quadrado ambos os membros da igualdade a = (m/n) b,
teremos:
a2 = (m2
/ n2 ) . b2
2b2 = (m2
/ n2 ) . b2
Logo, m2 / n2=2
Donde: m2 = 2 n2
Como m é par, segue-se que m2 é
divisível por 4, o mesmo ocorrendo com 2 n2
Logo, n2 é divisível por 2
e n também, o que contradiz a hipótese de que n é ímpar.
A existência do irracional vinha abalar o
edifício pitagórico, que considerava todas as medidas como dadas por números
discretos de mônadas. Esse abalo iria levar a ciência grega para o imobilismo,
o qualitativo e a forma. Na Matemática, para a Geometria.
Logo, viria Platão.
Prosseguir
Voltar
|